Por que non dividimos por cero?

Os lectores poden preguntarse por que dedico un artigo enteiro a un asunto tan banal? O motivo é o asombroso número de estudantes (!) que realizan casualmente a operación baixo o nome. E non só estudantes. Ás veces pego e profesores. Que serán capaces de facer os alumnos deste tipo de profesores en matemáticas? O motivo inmediato para escribir este texto foi unha conversación cun profesor para o que a división por cero non era un problema...

Con cero, si, excepto pola molestia de nada, porque realmente non necesitamos usalo na vida cotiá. Non imos mercar cero ovos. "Hai unha persoa na sala" soa dalgún xeito natural e "cero persoas" soa artificial. Os lingüistas din que o cero está fóra do sistema lingüístico.

Tamén podemos prescindir do cero nas contas bancarias: basta con usar, como nun termómetro, vermello e azul para valores positivos e negativos (ten en conta que para a temperatura é natural usar o vermello para os números positivos e para as contas bancarias). é ao revés, porque o débito debería activar un aviso, polo que o vermello é moi recomendable).

Ao incluír o cero como número natural, tocamos o problema da diferenciación Números cardinais od doméstico. Dentro de 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, ....

a potencia do número é a mesma que o número do lugar onde se atopa. En caso contrario, xa está na secuencia 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, ....

O número de conxuntos singleton é segundo, o número de conxuntos con dous elementos é terceiro, e así por diante. Temos que explicar por que, por exemplo, non numeramos dende cero as prazas dos deportistas nas competicións. Entón o primeiro clasificado recibiría unha medalla de prata (o ouro foi para o gañador do cero), etc. No fútbol utilizouse un procedemento un tanto semellante: non sei se os lectores saben que "liga un" significa " seguindo o mellor". ", e a liga cero está chamada a converterse na "liga maior".

Ás veces escoitamos o argumento de que hai que comezar de cero, porque é conveniente para os informáticos. Continuando con estas consideracións, debería cambiarse a definición de quilómetro: debería ser 1024 m, porque este é o número de bytes nun kilobyte (referireime a unha broma coñecida polos científicos informáticos: "Cal é a diferenza entre un novo e un un estudante de informática e un estudante de quinto curso desta facultade? que un kilobyte son 1000 kilobytes, o último - que un quilómetro son 1024 metros")!

Outro punto de vista, que xa se debe tomar en serio, é este: medimos sempre dende cero! Basta con mirar calquera escala na regra, na báscula doméstica, mesmo no reloxo. Dado que medimos desde cero, e contar pode entenderse como unha medida cunha unidade adimensional, entón debemos contar desde cero.

É un asunto sinxelo, pero...

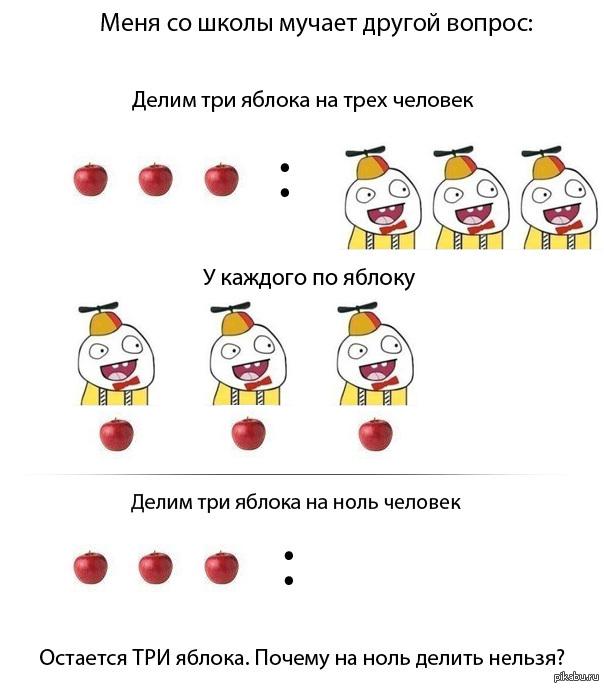
Deixamos o razoamento xeral e volvamos á división por cero. O asunto é sinxelo e sería sinxelo se non fose por... e que? Pensemos e probemos. Canto pode ser - un dividido por cero? Vexamos: 1/0 = x. Multiplica os dous lados polo denominador do lado esquerdo.

Temos 1=0. Algo anda mal! Que pasou? Ah, supoño! A suposición de que hai un cociente de unidade e cero leva a unha contradición. E se un non se pode dividir por cero, outro número pode. Se, lector, encolle os ombreiros e te preguntas por que o autor (é dicir, eu) escribe sobre tales banalidades, entón... Alégrome moito!

A fórmula 0/0 = 0 podería defenderse de forma teimosa, pero contradí a regra de que o resultado de dividir un número por si mesmo é igual a un. Absolutamente, pero moi diferentes son símbolos como 0/0, °/° e similares no cálculo. Non significan ningún número, senón que son designacións simbólicas para determinadas secuencias de certos tipos.

Nun libro de enxeñería eléctrica, atopei unha comparación interesante: dividir por cero é tan perigoso como a electricidade de alta tensión. Isto é normal: a lei de Ohm establece que a relación entre a tensión e a resistencia é igual á corrente: V = U / R. Se a resistencia fose cero, polo condutor circularía unha corrente teoricamente infinita, queimando todos os condutores posibles.

Unha vez escribín un poema sobre os perigos de dividir por cero para todos os días da semana. Lembro que o día máis dramático foi o xoves, pero é unha mágoa por todo o meu traballo neste ámbito.

Cando divides algo por cero

Luns moi cedo

Semana o que acaba de pasar

Xa fracasaches estrepitosamente.

Cando o martes pola tarde

Pon cero no denominador

Xa che digo, estás equivocado

Mal matemático!

Cando pasa por cero, pola perversión,

Queres separar o mércores

Terás moitos problemas

Tes feno e auga na cabeza!

Un tal Bartek estivo connosco.

Estaba en desacordo coas regras.

O xoves, é divisible por cero.

Xa non está entre nós!

Se un desexo estraño se apodera de ti

Divide por cero o venres

Serei sincero, serei sincero:

Mal comezo desta fin de semana.

Cando é cero, nalgún lugar do sábado

O divisor será teu (non en negrita)

Axeonllarse baixo o valado da igrexa.

Esta é a túa resurrección.

Queres cero baixo o guión,

Fai un festivo o domingo

Trae tiza, pizarra negra.

Escribe: non é divisible por cero!

O cero asóciase ao baleiro e á nada. En efecto, chegou ás matemáticas como unha cantidade que, ao engadirse a calquera, non a cambia: x + 0 = x. Pero agora cero aparece en varios outros valores, sobre todo como inicio de escala. Se fóra da xanela non hai nin temperatura positiva nin xeadas, entón ... isto é cero, o que non significa que non haxa temperatura en absoluto. Un monumento de clase cero non é aquel que foi demolido durante moito tempo e simplemente non existe. Pola contra, é algo así como o Wawel, a Torre Eiffel e a Estatua da Liberdade.

Ben, a importancia do cero nun sistema posicional dificilmente se pode sobreestimar. Sabes, lector, cantos ceros ten Bill Gates na súa conta bancaria? Non sei, pero gustaríame a metade. Ao parecer, Napoleón Bonaparte notou que as persoas son coma ceros: adquiren significado pola posición. Na película de Andrzej Wajda As the Years, As the Days Go by, o apaixonado artista Jerzy estala: "O filisteo é cero, nihil, nada, nada, nihil, cero". Pero cero pode ser bo: a "desviación cero da norma" significa que todo vai ben, e segue así!

Volvamos ás matemáticas. O cero pódese sumar, restar e multiplicar impunemente. "Engañei cero quilogramos", di Manya a Anya. "E isto é interesante, porque perdín o mesmo peso", responde Anya. Entón, imos comer seis porcións cero de xeado seis veces, non nos vai facer mal.

Non podemos dividir por cero, pero podemos dividir por cero. Pódese repartir facilmente un prato de boliñas cero aos que están esperando comida. Canto recibirá cada un?

O cero non é positivo nin negativo. Este e o número non positivoи non negativo. Cumpre as desigualdades x≥0 e x≤0. A contradición "algo positivo" non é "algo negativo", senón "algo negativo ou igual a cero". Os matemáticos, en contra das regras da lingua, sempre dirán que algo é "igual a cero" e non "cero". Para xustificar esta práctica, temos: se lemos a fórmula x = 0 "x é cero", entón x = 1 lemos "x é igual a un", que podería ser tragado, pero que pasa con "x = 1534267"? Tampouco pode asignar un valor numérico ao carácter 0⁰nin elevar o cero a unha potencia negativa. Por outra banda, pode enraizar cero a vontade... e o resultado sempre será cero. 

Función exponencial y = a^x, a base positiva de a, nunca pasa a ser cero. Segue que o logaritmo cero non existe. De feito, o logaritmo de a á base b é o expoñente ao que se debe elevar a base para obter o logaritmo de a. Para a = 0, non existe tal indicador e cero non pode ser a base do logaritmo. Porén, o cero no "denominador" do símbolo de Newton é outra cousa. Supoñemos que estas convencións non dan lugar a unha contradición.

evidencia falsa

A división por cero é un tema común para as probas falsas, e páselles incluso a matemáticos experimentados. Permíteme darche dous dos meus exemplos favoritos. O primeiro é alxébrico. Vou "probar" que todos os números son iguais. Supoñamos que hai dous números que non son iguais. Polo tanto, un deles é maior que o outro, sexa a > b. Supoñamos que c é a súa diferenza

c \uXNUMXd a - b. Entón temos a - b = c, de onde a = b + c.

Multiplicamos as dúas partes desta última por a - b:

a² – ab = ab + ac – b2 – bc.

Traduzo ak ao lado esquerdo, por suposto que lembro o cambio de signo:

a² - ab - ac = ab - b2 - bc.

Excluín factores comúns:

A (a-b-c) \uXNUMXd b (a-b-c),

Comparto e teño o que quería:

a = b.

E en realidade aínda máis estraño, porque asumín que a > b, e teño que a = b. Se no exemplo anterior "enganar" é fácil de recoñecer, entón na demostración xeométrica de abaixo non é tan fácil. Vou demostrar que... o trapecio non existe. A figura chamada comunmente trapecio non existe.

Pero supoña primeiro que existe un trapecio (ABCD na figura de abaixo). Ten dous lados paralelos ("bases"). Estiramos estas bases, como se mostra na imaxe, para obter un paralelogramo. As súas diagonais dividen a outra diagonal do trapecio en segmentos cuxas lonxitudes se indican x, y, z, como en figura 1. Da semellanza dos triángulos correspondentes obtemos as proporcións:

onde definimos:

Oraz

onde definimos:

Reste os lados da igualdade marcados con asteriscos:

 Acurtando ambos os dous lados en x − z, obtemos – a/b = 1, o que significa que a + b = 0. Pero os números a, b son as lonxitudes das bases do trapecio. Se a súa suma é cero, tamén son cero. Isto significa que unha figura como un trapecio non pode existir! E como os rectángulos, os rombos e os cadrados tamén son trapecios, entón, querido lector, tampouco hai rombos, rectángulos e cadrados...

Adiviña Adiviña

Compartir información é a máis interesante e desafiante das catro actividades básicas. Aquí, por primeira vez, atopámonos cun fenómeno tan habitual na idade adulta: “adiviña a resposta, e despois comproba se acertaches”. Isto é moi acertadamente expresado por Daniel K. Dennett (“How to Make Mistakes?”, en How It Is – A Scientific Guide to the Universe, CiS, Varsovia, 1997):

Este método de "adiviñar" non interfire coa nosa vida adulta, quizais porque o aprendemos cedo e adiviñar non é difícil. Ideoloxicamente, o mesmo fenómeno ocorre, por exemplo, na indución matemática (completa). No mesmo lugar, "adiviñamos" a fórmula e despois comprobamos se a nosa suposición é correcta. Os alumnos sempre preguntan: “Como coñecimos o patrón? Como se pode sacar?" Cando os estudantes me fan esta pregunta, converto a súa pregunta nunha broma: "Séino porque son un profesional, porque me pagan por saber". Os alumnos da escola poden ser contestados no mesmo estilo, pero máis en serio.

Exercicio. Teña en conta que comezamos a suma e a multiplicación escrita coa unidade máis baixa e a división coa unidade máis alta.

Unha combinación de dúas ideas

Os profesores de matemáticas sempre sinalaron que o que chamamos separación de adultos é a unión de dúas ideas conceptualmente diferentes: Vivenda i separación.

O primeiro (Vivenda) ocorre en tarefas onde o arquetipo é:

Dividir-dividir Estas son tarefas como:

? (Conservamos o estilo orixinal deste problema, tomado do manual de Julian Zgozalewicz publicado en Cracovia en 1892 - o złoty é o złoty renano, a moeda que estivo en circulación no Imperio Austro-Húngaro ata principios do século XX).

Agora considere dous problemas con o libro de texto de matemáticas máis antigo en polaco, pai Tomasz Clos (1538). É unha división ou un coupé? Resolve-lo como deberían os escolares do século XIX:

(Tradución do polaco ao polaco: hai un litro e catro potas nun barril. Unha pota son catro cuartos. Alguén comprou 20 barrís de viño por 50 zł para o comercio. Os impostos e impostos (graves especiais?) serán de 8 zł. vender un cuarto para gañar 8 zł?)

Deportes, física, congruencia

Ás veces nos deportes hai que dividir algo por cero (cociente de goles). Ben, os xuíces dalgunha maneira tratan con iso. Porén, en álxebra abstracta están na axenda. cantidades distintas de cerocuxo cadrado é cero. Incluso se pode explicar de forma sinxela.

Considere unha función F que asocia un punto (y, 0) cun punto no plano (x, y). Que é F², é dicir, unha dobre execución de F? Función cero: cada punto ten unha imaxe (0,0).

Finalmente, as cantidades distintas de cero cuxo cadrado é 0 son un pan case diario para os físicos, e os números da forma a + bε, onde ε ≠ 0, pero ε² = 0, chaman os matemáticos números dobres. Ocorren na análise matemática e na xeometría diferencial.

Despois de todo, hai algo en aritmética que ten división por cero polo menos no nome. Vén de congruencia. Denote Z o conxunto de números enteiros. Dividir o conxunto Z por p significa que igualamos cada número (enteiro) a algúns outros, é dicir, a aqueles polos que a súa diferenza é divisible. Entón, cando temos cinco tipos de números correspondentes aos números 0, 1, 2, 3, 4 - os posibles restos ao dividirse por 5. A fórmula escríbese así:

mod cando a diferenza é múltiple.

Para = 2, só temos dous números: 0 e 1. Dividir números enteiros en dúas clases deste tipo é equivalente a dividilos en pares e impares. Substitúmolo agora. A diferenza sempre é divisible por 1 (calquera número enteiro é divisible por 1). É posible tomar =0? Probemos: cando a diferenza de dous números é múltiplo de cero? Só cando estes dous números son iguais. Entón, dividir un conxunto de números enteiros por cero ten sentido, pero non é interesante: non pasa nada. Non obstante, hai que subliñar que non se trata dunha división de números no sentido que se coñece dende a escola primaria.

Tales accións están simplemente prohibidas, así como as matemáticas longas e amplas.

Arroz. 2. Identificación de números mediante a comparación

(modo 5 e modo 2)